【抄訳】Olkin-Pratt推定量の論文 Julian Karch (2020)

次の論文を紹介します．

Karch, J. (2020). Improving on Adjusted R-Squared. Collabra: Psychology, 6(1): 45. DOI: https://doi.org/10.1525/collabra.343

決定係数，自由度調整済決定係数に代わる推定量として，Olkin-Pratt推定量を使うことを提案している．こちらはUMV不偏推定量である（[Olkin and Pratt, 1958]）．使われなかった理由としては計算が難しいと思われていた（超幾何級数が出てくる）ことが挙げられるであろうが，著者は全くそうではないことを示し，本人のRパッケージに実装した！非常に痛快な論文だと感じた．

また，理論系の人間としては，こんなにきれいなIMRD構成の論文を初めて読んだ．

Abstract

回帰平方和 (Explained Sum of Squares) は線型重回帰模型の当てはまりの良さを定量化する指標として一般的である．一般にいう「自由度調整済決定係数 (adjusted R-squared)」は偏倚を受けている(biased)という欠点がある．一方でOlkin-Pratt推定量は最適で不偏である．しかしながら，計算が難しいという点で広くは使われてこなかった．本論文では，正確で高速な算譜を提案し，広い実用に供する．続いてOlkin-Pratt推定量と自由度調整済決定係数と他18の推定量を数値シミュレーションを用いて性能比較をした．結果，Olkin-Pratt推定量は標準的な計量の下で最適であった（全ての不偏推定量の中で平均自乗誤差が小さい）．一方で，全ての推定量の中で平均自乗誤差が小さい推定量はどれか？という問題については最適なものが見つからなかった．これらの結果に基づいて，どの状況ではどの推定量を用いるべきかについて議論した．また，Olkin-Pratt推定量を始めとした上述の推定量を計算するRパッケージaltR2を準備した．

Introduction

SPSSやRのlm関数などは寄与率と自由度調整済寄与率の機能しか持たない．以前から（特に [Raju, Bilgic, Edwards and Fleer 1997] 以来）他の推定量との性能比較の研究はなされていた．この研究もその類であるが，次の３点が違う．

  • 新たに Olkin-Pratt推定量を加えた（[Olkin and Pratt, 1958] Unbiased Estimation of Certain Correlation Coefficients ）．これはUMV推定量である．
  • Raju et alが「有効性」の定義を不明瞭にしていた点を，Lehmann and Casella 2003を参考に修正した．
  • 比較した総ての推定量を含んだRパッケージaltR2を用意した．

ここで第一点のOlkin-Pratt推定量が肝要だと推測するが，これをどうして決定係数の代替とみなせるのかの議論は極めて非自明だと思う．

Method

線型重回帰模型

    \[Y=\beta_0\boldsymbol{1}<em>n+X\beta+\epsilon,\qquad X\in M</em>{Np}(\R),\;\epsilon\sim\mathrm{N}<em>N(0,\sigma^2</em>\epsilon I_n).\]

を考える．すると Y に正規分布の仮定を置いている事となり，その真の分散を \sigma_Y^2 としたとき，

    \[\rho^2:=1-\frac{\sigma^2_\epsilon}{\sigma^2_{Y}}\]

を自乗多重相関係数という． \sigma_\epsilon^2,\sigma^2_Y は未知だから，最尤推定量＝OLS推定量を代入したものを \widehat{\sigma}<em>\epsilon^2,\widehat{\sigma}</em>{Y}^2 としたとき，これを変わりに用いたもの

    \[R^2:=1-\frac{\widehat{\sigma}^2_\epsilon}{\widehat{\sigma}^2_{Y}}\]

を決定係数という．これに修正を加えたいとするならば，まず \widehat{\sigma}^2_\epsilon,\widehat{\sigma}^2_Y のいずれも \sigma^2_\epsilon,\sigma^2_Y の不偏推定量ではない，という点に注目する必要がある．不偏分散と同じ発想で，自由度に関して調整して

    \[\widehat{\rho}^2_E(R^2)=1-\frac{SS_R/(N-p-1)}{SS_T/(N-1)}=1-\frac{N-1}{N-p-1}(1-R^2)\]

を 自由度調整済決定係数またはEzekiel統計量という．しかし全体としてはこれも自乗多重相関係数の不偏推定量ではない．この問題に対して，実は [Olkin and Pratt, 1958] がUMV不偏推定量を与えていた．

[Alf and Graf, 2002] が R^2 の最尤推定量を与えているが，UMV不偏推定量の前にはどうも出来ない！（そもそも不偏なのかな？）．なお，いま挙げたすべては一致性は持つ．

筆者も

No such strong theoretical justification exists for any other estimator.

とコメントしている．同時に，いままで使われていなかった理由として，

Despite this favorable property, the Olkin-Pratt estimator has not been implemented in any software package, is not being used, and has not been included in any previous comparison. The reason for this is that it has been believed to be difficult to compute (Shieh, 2008) since its formula contains the hypergeometric function. The hypergeometric function {}_2F_1(a, b; c; z) is difficult to compute as it is defined via an infinite series.

なお，論文で “exact Olkin-Pratt estimator” とあるのは，正確な Olkin-Pratt推定量のことで，超幾何関数の級数表示で，第 k 項で切ったものを用いた場合の Olkin-Pratt推定量の近似にあたるものはすでに以前の比較研究で用いられていたことがあったので，これと区別するための表現である．

また”positive-part estimator”とは，例えばOlkin-Pratt推定量については[Olkin and Pratt, 1958]が第１節のIntroductionで述べている通り，負の値をとり得る．これは最尤推定量と R^2 を除いてみなそうである．そこで，[Shieh, 2008] では正部分のみを取ることを提案した．これは偏倚を増すが，平均自乗誤差を減らす．

数値実験については，上述も含めた計20の推定量を， \rho,N,p を変えて実験した．これは，[Fisher (1928) The General Sampling Distribution of the Multiple Correlation Coefficient ] によれば 標本自乗多重相関係数 R^2 の分布を変えるただ３つの要因だからである．

  • N=10,20,30,40,50,60,100,150 ．これは1995-2006に発表された心理学研究のサンプルサイズの75%をカバーすると推定されている．このうち60以下のものが半分以上である．
  • p=2,5,10 ．これは過去の比較研究に倣った．
  • \rho^2=0.0,0.1,\cdots,0.9 に加えて \rho^2=0.01,0.05．極めて小さい多重相関係数は心理学において多く見られるためである．

心理学研究のサンプルサイズについては初めて知った……．

Result

種々の枠組みの下で数値実験を行っている．

  • UMV不偏性の観点からはOlkin-Pratt推定量の全勝である．

The exact Olkin-Pratt estimator was the only estimator that was empirically unbiased across all conditions. Additionally, only approximations of the exact Olkin-Pratt estimator were empirically unbiased in any condition, namely: the Olkin-Pratt K = 2, K = 5, and the Pratt estimator.

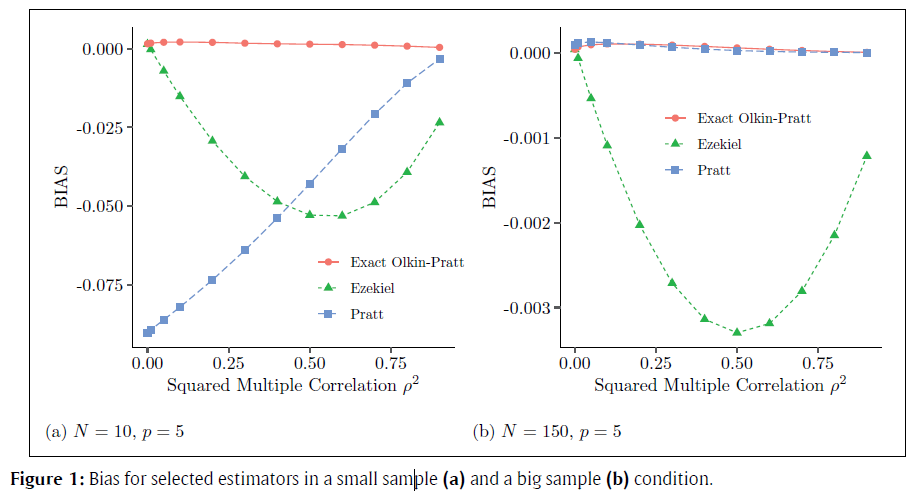
  • 「全推定量の中でUMVであるか？」という観点からは，「全ての状況においてベスト」という推定量は存在しなかった．「特定の状況においてベスト」だったのは６つの推定量のみで，正のEzekiel推定量，Smith, Wherry, Claudyと最尤推定量と通常の決定係数 R^2．
    • 一般に，真の値 \rho が事前に判っている状況でない限り，どの推定量を使うのが良いということが一概にいえない．特にデータが少ない場合である．
    • データが多い場合に R^2 の誤差が大きくなっていることが判り，それ以外の推定量には特に遜色がない．
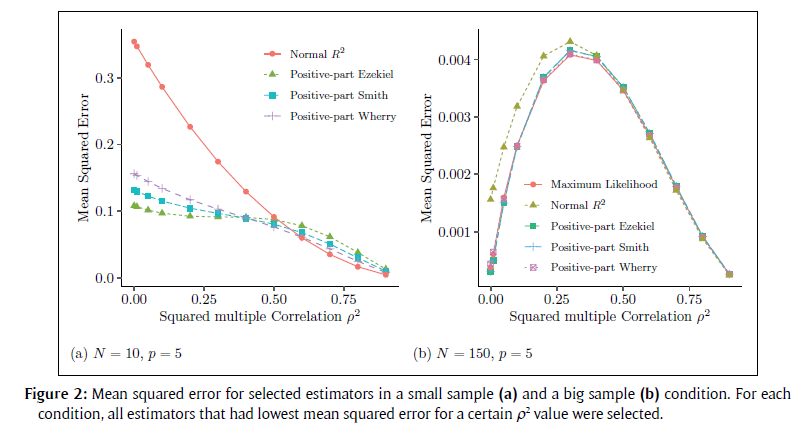
  • そこで「どの状況でも平均自乗誤差がより小さい」という優越関係が見られるかに注目すると，
    • 全ての推定量について，正部分を取ることは平均自乗誤差を一様に改善した（当然だろう）．
    • Olkin-Pratt推定量は，より近似が粗いほど，平均自乗誤差は一様に改善される．
    • これ以外に意味のある示唆は殆ど得られない．SmithがEzekielに優ることくらいか．
  • 続いて，最悪自乗誤差が小さい推定量がどれかを見る．
    • 正のEzekiel推定量，Wherryと最尤推定量と R^2 が特定の状況で最悪自乗誤差が一番小さかった．
    • 最悪自乗誤差の全24状況での平均は正のEzekiel推定量が最も小さかった．最尤推定量に10%ほどの差を付けている．
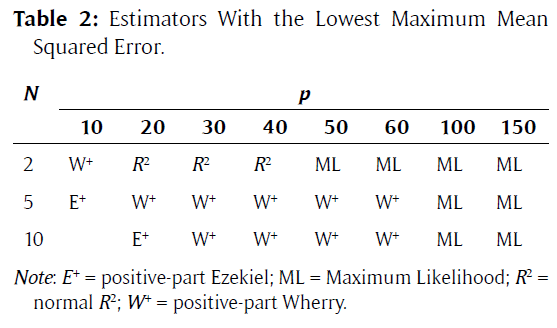
  • 平均自乗誤差の平均で比較してみる．
    • 正のEzekiel推定量，Smith, Wherryと最尤推定量が特定の状況で最良であった．
    • 平均自乗誤差の全24状況での平均は正のEzekiel推定量が最も小さかったが，最尤推定量もほぼ変わらない．

というように，正のEzekiel推定量の活躍がめぼしいので，あらゆる状況で，ベストの推定量とどれくらい平均自乗誤差が大きいかを見てみたところ，最悪平均自乗誤差が決して11%以上大きいことはなく，平均自乗誤差の平均が4%以上高いことはなかった．悪くない選択と言えるだろう．

Discussion and Conclusion

UMV (Uniformly Minimum Variance) の観点からはOlkin-Pratt推定量の圧勝であり，この意味で常にOlkin-Pratt推定量を使うべきである．

しかし不偏性を必要とせず，平均自乗誤差のみを気にするならば，どの推定量が良いかということは一概には言えない．当然一様に良いものは存在しないし，「最悪の平均自乗誤差」と「平均自乗誤差の平均」との観点からも，一様に良いものは存在しない．が，「最悪の平均自乗誤差」と「平均自乗誤差の平均」の両方の観点から概して良いだろうと言えるものは，Ezekiel推定量（自由度調整済決定係数）の正部分であった．

もし \rho^2 の値について事前に知識があるならば，本論文の詳細な結果を確認して，その状況の下でベストな推定量を選ぶことが出来るが， \rho^2 の値が全くの未知である場合も，「最悪の平均自乗誤差」と「平均自乗誤差の平均」のそれぞれの観点からの比較の詳細を見て，正のEzekiel推定量，Smith, Wherryと最尤推定量と R^2 の中から選ぶことが出来る．筆者は個人的に（主語 I を用いて）正のEzekiel推定量を推奨している．特に p\ll N の状況下では推定量の間に大きな差が見られないので，安牌であると言える．

不偏性と効率性のどちらをより重視すべきかも不明の状況下で，筆者は個人的に正確なOlkin-Pratt推定量を次の３つの理由から推奨している．

  • UMV不偏推定量であるという性質は，一般の回帰分析において標準的な見方からして「最適」である．そもそもOLS推定量を用いている理由も，これがUMV不偏推定量であるからである．（これはあまり強い理由になっていない気がする，OLS推定量は不偏とは限らない他の推定量と比べても効率が良い可能性がある点について検証していない）．
  • 心理学は伝統的に説明的なモデリングについてのものである．説明的なモデリングにおいては一般的に不偏性を重視すべきである [Shmueli, 2010]．
  • 不偏推定量を用いているならば，メタ分析など，データの数が多い状況ではどんどん効率がよくなってくる．他の推定量であるとこの美点はない．

似たような比較実験 [Yin and Fan, 2001] や [Shieh, 2008] ではPratt推定量を推奨してた．前者は Pratt と ClaudyによるOlkin-Pratt推定量の近似としか比較対象にしていない上に，不偏性しか見ていなかったから，正確なOlkin-Pratt推定量も考慮対象に入れたならば，これを推奨していただろう．一方で後者も，不偏性しか本質的には考慮せず，また計算の困難さも考慮に入れた．

本論文ではRパッケージを提供したために，もうShiehの枠組み（計算が困難な推定量を忌避すること）の利点はなくなっているだろう．

Conclusion

In conclusion, I recommend using the exact Olkin-Pratt estimator by default. However, if the researcher is confident that minimizing MSE is more critical than unbiasedness, then a different estimator should be used. In this case, I recommend an individualized choice based on the strategy described at the beginning of this discussion, and if this is not feasible or the sample size N is large compared to the number of predictors p, the positive-part version of the Ezekiel estimator.

あの

あの

数学科出身の統計家志望．

関連記事

関連記事

モデリングとシミュレーション

親族構造の生成

数学と人類学

「数学の人類学」の始まり

コメント

この記事へのコメントはありません。

カテゴリー

あの

あの

「あの」という名前でYouTube活動もしている数学科出身の統計家志望．

りん

りん

「りん」という名前であのちゃんのお世話をしながら、法律家を志してます。

107r57

土木工学者かつクイズプレイヤー．

アーカイブ一覧
TOP