次のデンマークでの国際会議での講義録の内容を抄訳した.
Cramér, Harald (1925) On Some Classes of Series Used in Mathematical Statistics Matematiker Kongressen i København 31. August — 4. September 1925: Den Sjette Skandinaviske Matematikerkongres.: Beretning Udgiven af Kongressens Organisationskomite 399-425
この文献は非常にアクセスが難しかったが,例えばここに正式名称が残っていて助かった.これを用いて大学のE-jornal Portalから検索を書けると,最終的にGale Primary SourcesのNineteenth Century Collections Onlineからデータが見つかり,読むことが出来た.Gram-Charlier展開やEdgeworth展開やなどの漸近展開の手法が最初に使われ始めた時期に書かれたレビューで,非常に歴史的な価値が高いと思ったので,どうしても読みたかった.ということで,読んだ際に付けたメモを以下に残すこととした.
歴史的な含意としては,スカンジナビアとドイツの天文学者が,誤差の解析を通じて漸近展開を使い始めた,ということが書いてある.スウェーデンの天文学者 Carl Charlier と Thorvald Thiele, Jørgen Pedersen Gram らデンマークのアクチュアリーと,ドイツは Heinrich Bruns などの天文学者が最初であったという.その数学的な基礎付けを与えようとしている文献である.
論文の内容の翻訳と,概略して済ませている地の文とが混じっており,少し読みづらい部分もあるかもしれない.
以下本文
統計を要請する科学分野で働くものの多くは,解くのに高度な数学知識を必要とする問題に出会うことがある.しかし何かしらの解決を見る必要がある訳で,それで統計はいつだって実践が理論に先行する.その例に昨今のスカンジナビアとドイツの数理統計で使われる無限級数の問題がある.
統計理論でこのような無限級数は,正規密度からの逸脱(deviation)の具合を表す解析的表示を求めるための問題を解くために使われる.そして正規密度は展開の初項と見られ,最初の3,4項を考えるだけで十分な正確さが得られるようだ.そしてこの級数は正規密度の導関数に係数をつけること繰り返すことで得られていく.このような級数はGram, Thiele, Bruns, Charlier, Edgeworthによって使われた.
![]() で近似する場合に議論を限り,
で近似する場合に議論を限り,
![Rendered by QuickLaTeX.com \[f(x)=\sum_{\nu=0}^\infty\frac{c_\nu}{\nu!}\varphi^{(\nu)}(x).\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-da4a5178d00940f29bb8d5576eee0b18_l3.png)
という形で考える.この形を指数級数(exponential series)と呼ぼう.
数学者が級数を見たらまず収束を問題にするだろうが,私はこれを二の次だと考える.なぜならあとで示すように,他に重要な問題があるからである.しかし,ここでは最初に収束の問題を議論したい.なぜならば,1921にSwedishアクチュアリー協会で指数級数について講義をした際に,Phragmen教授が,指数級数を用いて統計解析する人間が収束性について突飛なことをいうと文句を言っていたためである.[筆者注:どうやらデンマークの有名な教科書がミスっている]
指数級数の収束性
全く形式的に
![Rendered by QuickLaTeX.com \[f(x)\sim\sum_{\nu=0}^\infty\frac{c_\nu}{\nu!}\varphi^{(\nu)}(x),\qquad c_\nu=(-1)^\nu\int_\mathbb{R} fH_\nu dx.\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-d3ddc635a733d8fa6d9d71745b81ba2d_l3.png)
と期待出来る. ![]() の存在を認め,右辺の級数の収束を考えることが「収束性の問題」である.一般の標準化していない
の存在を認め,右辺の級数の収束を考えることが「収束性の問題」である.一般の標準化していない ![]() と
と ![]() の密度
の密度 ![]() については,
については,
![Rendered by QuickLaTeX.com \[F(x)\sim\sum_{\nu=0}^\infty\frac{k_\nu}{\nu!}\varphi^{(\nu)}(x),\qquad k_\nu=(-b)^\nu\int_\R F(x)H_\nu\left(\frac{x-a}{b}\right)dx.\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-996835e67d3ac44d746490ac76533160_l3.png)
第3節で ![]() -理論を解説し,
-理論を解説し, ![]() がHermite直交系に対して展開可能な十分条件を与えている.
がHermite直交系に対して展開可能な十分条件を与えている.
補題 (Hermite直交系に対するParsevalの補題 Weyl 1909).![]() について,
について,
![Rendered by QuickLaTeX.com \[f\sim\sum_{\nu=0}^\infty\frac{c_\nu}{\nu!}\varphi^{(\nu)}(x),\quad g\sim\sum_{\nu=0}^\infty\frac{\gamma_\nu}{\nu!}\varphi^{(\nu)}.\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-b9e4a46010d399b683d5b5a1dbde23d5_l3.png)
ならば,
![Rendered by QuickLaTeX.com \[\int_\R f(x)g(x)e^{\frac{x^2}{2}}dx=\frac{1}{\sqrt{2\pi}}\sum_{\nu=0}^\infty\frac{c_\nu\gamma_\nu}{\nu!}.\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-520f05cfe1723b6b818bb844fe1d263a_l3.png)
定理.
![]() は
は![]() を満たすならば,
を満たすならば,
![Rendered by QuickLaTeX.com \[f(x)=\sum_{\nu=0}^\infty\frac{c_\nu}{\nu!}\varphi^{(\nu)}(x),\qquad x\in\R,c_\nu=(-1)^\nu\int_\R f(x)H_\nu(x)dx.\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-ae2528b0a93c4aeb7030796790625087_l3.png)
が成り立ち,右辺の級数は一様に絶対収束する.
第4節ではGalbrunによる総和核の方法を紹介し,Diniの定理のような ![]() に収束しますという結論と広義一様収束性を得るが「仮定は緩まったけど,級数の絶対収束性がわからないから,結論も弱まった」とまとめている.
に収束しますという結論と広義一様収束性を得るが「仮定は緩まったけど,級数の絶対収束性がわからないから,結論も弱まった」とまとめている.
第5節
数理統計の書物に通じている人は,すぐに上述の結果は書物に見られるより緩い仮定しか採用していないことに気づくであろう.実はこれ以上仮定を緩めることは出来ない.
![]()
という場合を考える.![]() であり,
であり,
![]()
より,![]() ならば定理の要件を満たすことが判る.
ならば定理の要件を満たすことが判る.
一方で,![]() の計算を通じて
の計算を通じて
![Rendered by QuickLaTeX.com \[f(0)=\frac{1}{\sqrt{2\lambda}}\sum_{\nu=0}^\infty\frac{(2\nu)!}{2^{2\nu}(\nu!)^2}\paren{1-\frac{1}{2\lambda}}^\nu.\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-f9a81a5adcc3968ffef59b2f9eb56430_l3.png)
を得るが,これは![]() で絶対収束,
で絶対収束,![]() で発散という振る舞いをする.
で発散という振る舞いをする.
第6節
こうして,収束性の問題の扱いは随分と杜撰であったことがわかるだろう.その理由の1つは,Hermite多項式と指数級数との定義が著者によってバラバラであることにあると考える.
筆者は第7節で,第3,4節の結果を一般の ![]() の場合の結論に拡張して見せる.
の場合の結論に拡張して見せる.
指数級数の漸近的性質と根源誤差の仮定
数学の議論をしてきたが,基礎付けの点で重要でも,応用上真に重要なのは収束性ではない.
実用上は最初の4,5項しか用いないことを思い起こしてほしい.そもそも,関心のある確率変数 ![]() を標準化することで,正規密度の1次と2次の導関数の項は消えるため,正規近似で随分良い精度を叩き出す.
を標準化することで,正規密度の1次と2次の導関数の項は消えるため,正規近似で随分良い精度を叩き出す.
そこで次の問題に分け入っていくことになる「密度 ![]() のクラスであって,上述したような,指数級数展開の最初の数項で十分良い近似が与えられるようなクラスはどのようなものか?」
のクラスであって,上述したような,指数級数展開の最初の数項で十分良い近似が与えられるようなクラスはどのようなものか?」
Is there a general class of statistical frequency-functions, which are able to be approximately represented by the first few terms of an exponential series?
つまり,収束性より,漸近的性質に興味がある. ![]() の部分和についての極限より,
の部分和についての極限より, ![]() の極限に興味がある.
の極限に興味がある.
この研究を始めるには,まず一般の密度について詳しく知る必要がある.というのも,このような漸近解析がなされるのは,特定の確率分布が生じてくる因果構造に対するモデルを考えている際なのであって,その際に ![]() は特殊な構造を持つ.
は特殊な構造を持つ.
例えば,このような漸近解析は最初に誤差論で(そして現状は誤差論のみで)なされた.誤差の分布に正規分布が出現するのはなぜか?という疑問に,ある種の回答を与える理論で,歴史的にはLaplaceによって初めて扱われ,その後は根源誤差の仮説(hypothesis of elementary errors)と呼ばれている.
つまり,密度 ![]() を持つ確率変数は,膨大な確率変数の独立和として与えられていると仮定して解析を開始する.しかしこの仮定の下でのいままでの漸近解析は形式的な議論のみで,数学的には極めて怪しい.しかしその状態でも応用上は,形式的に得られた漸近展開の最初の数個の微小項を計算に入れることで,精度が十分改善されることが度々観察される.
を持つ確率変数は,膨大な確率変数の独立和として与えられていると仮定して解析を開始する.しかしこの仮定の下でのいままでの漸近解析は形式的な議論のみで,数学的には極めて怪しい.しかしその状態でも応用上は,形式的に得られた漸近展開の最初の数個の微小項を計算に入れることで,精度が十分改善されることが度々観察される.
しかし,この実用上の利益に満足せずさらに一歩踏み込んで「これが,誤差に関する根源誤差の仮説の証左の一つである」と論証したり,漸近展開の係数に現れるキュムラントなど(例えば歪度や尖度)を確率分布の特徴付けに使いたいならば,数学的な基礎付けが要請されるのである.
第九節
この節では数学的な定式化を与えている.
根源誤差 ![]() の分布関数を
の分布関数を ![]() で表す.すると,誤差
で表す.すると,誤差 ![]() の分布関数は
の分布関数は ![]() の畳み込みが与える.各
の畳み込みが与える.各 ![]() は平均
は平均 ![]() で分散
で分散 ![]() を持つと仮定しても,一般性は失われない.すると,
を持つと仮定しても,一般性は失われない.すると, ![]() の分散は
の分散は ![]() が与え,
が与え, ![]() は変数
は変数
![]()
の分布関数を与え,これは平均 ![]() で分散
で分散 ![]() である.
である.
さて,誤差論によると, ![]() が十分大きいとき,
が十分大きいとき, ![]() は正規分布関数で近似できる.これは,第3節の知識からも説明出来る.
は正規分布関数で近似できる.これは,第3節の知識からも説明出来る. ![]() の指数級数展開を考えると,
の指数級数展開を考えると, ![]() の項は消えるため,
の項は消えるため,
![Rendered by QuickLaTeX.com \[W(x)\sim\Phi(x)+\sum_{\nu=3}^\infty\frac{c_\nu}{\nu!}\Phi^{(\nu)}(x),\qquad c_\nu=\frac{(-1)^\nu}{\nu}\int_\R H_\nu(x)dW(x).\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-e4de69ea5edba4d4d97e56827991c4bb_l3.png)
を, ![]() かつある
かつある ![]() について
について ![]() ならば得る.ただし,ここで各
ならば得る.ただし,ここで各 ![]() は存在するとは限らないものとする.ただし,
は存在するとは限らないものとする.ただし, ![]() 次の積率が存在するためには,
次の積率が存在するためには, ![]() が存在することが必要であることに注意.
が存在することが必要であることに注意.
第十節
この節では第九節で得た数学的定式化を用いて,第八節で提起した問題の枠組みを定める.
問題は次の通りである.十分大きな ![]() について,
について,
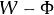 は小さい.
は小さい. の極限について,漸近的にいくつかの
の極限について,漸近的にいくつかの
で近似できる.![Rendered by QuickLaTeX.com \[\frac{c_3}{3!}\Phi^{(3)}(x)+\frac{c_4}{4!}\Phi^{(4)}(x)+\cdots+\frac{c_h}{h!}\Phi^{(h)}(x)\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-8be0e701e3c7ebeb6441c91564e22391_l3.png)
のは,それぞれ, ![]() がどのような性質を満たすときか?
がどのような性質を満たすときか?
この問題は保険会社のリスク管理の問題でも重要な意味を持つ.ここの根源誤差 ![]() を個々の保険契約での損失・利益の揺らぎと見るのである.多くの場合,
を個々の保険契約での損失・利益の揺らぎと見るのである.多くの場合, ![]() による一時近似では精度が足りないのである.
による一時近似では精度が足りないのである.
第十一節
第一の問題に答えていこう. ![]() が小さくなる,すなわち
が小さくなる,すなわち ![]() の極限で
の極限で ![]() に収束するのはいつか?この問題は多くの研究者が既に取り組んでおり,十分一般的な状況下で成り立つようである.
に収束するのはいつか?この問題は多くの研究者が既に取り組んでおり,十分一般的な状況下で成り立つようである.
ここでは次の場合に限って考えてみよう.各根源誤差 ![]() は3次の絶対積率
は3次の絶対積率
![]()
を持つとし,和を ![]() とする.すると,
とする.すると, ![]() が成り立つとき,
が成り立つとき, ![]() が
が ![]() 上一様に成り立つ.
上一様に成り立つ.
もし ![]() が
が ![]() に依らない,
に依らない, ![]() が同分布であるときは,次のような鋭い評価も得る:
が同分布であるときは,次のような鋭い評価も得る:
![]()
ただし, ![]() は
は ![]() に依らない定数である.
に依らない定数である.
さらに一般的な定理が,Liapunov, Lindeberg, Levyらによって得られている.これらは例えば,積率に関する要件は, ![]() -次の積率の存在のみを課した状態でも,
-次の積率の存在のみを課した状態でも, ![]() の
の ![]() への収束が保証出来る,というような結果である.なお,本当に
への収束が保証出来る,というような結果である.なお,本当に ![]() -次の積率しか存在しないならば,指数級数のあらゆる係数
-次の積率しか存在しないならば,指数級数のあらゆる係数 ![]() は無限大に発散するので,漸近解析は出来ないことになる.
は無限大に発散するので,漸近解析は出来ないことになる.
第十二節
第二の問題に答えていく.つまり, ![]() がいくつかの階数について,積率を持つとする.実は,
がいくつかの階数について,積率を持つとする.実は, ![]() が同分布であるときは,
が同分布であるときは,
![]()
が成り立つ.同分布でない場合も,その積率についてある種の正則性条件を満たすならば,やはりこのオーダーを持つ.

ではこれで,元の指数級数が漸近展開を与えるか?というと,実は違う.これをBernoulliの変数の場合を通じて見てみよう.
![]() としたとき,
としたとき,
![]()
となる.この分布関数のグラフは,
![]()
にて,幅
![]()
のジャンプをする階段関数になっている.実はこのジャンプ幅が ![]() のオーダーを持つため,
のオーダーを持つため,
![Rendered by QuickLaTeX.com \[\left|W(x)-\Phi(x)-\sum_{\nu=3}^h\frac{c_\nu}{\nu!}\Phi^{(\nu)}(x)\right|<\frac{K}{n^\alpha}.\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-1647d0648ea6e133620ccdaf19cdf78a_l3.png)
という形の結果は, ![]() については,
については, ![]() をどのようにとっても成り立たないことが判る.
をどのようにとっても成り立たないことが判る. ![]() の場合は
の場合は
![]()
という結果を得る.つまり,この場合の ![]() は,漸近展開をしても,正規近似以上の近似精度を得られないということである.
は,漸近展開をしても,正規近似以上の近似精度を得られないということである.
特に ![]() の場合が興味深い.このとき
の場合が興味深い.このとき ![]() となり,
となり, ![]() の項は全て消えている.しかしこのときでも残差
の項は全て消えている.しかしこのときでも残差
![Rendered by QuickLaTeX.com \[W(x)-\Phi(x)-\sum_{\nu=3}^h\frac{c_\nu}{\nu!}\Phi^{(\nu)}(x)\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-ff11b6450c50b1c98a60b711c087f793_l3.png)
は ![]() のオーダーを持つ.
のオーダーを持つ.
このような状況は, ![]() が離散分布だから,というわけでは別にない.
が離散分布だから,というわけでは別にない.
![]()
という混合正規分布についても同様の状況が起こる.というのも,特に ![]() が同分布の場合,
が同分布の場合, ![]() の指数級数展開は
の指数級数展開は ![]() 上一様に絶対収束するが,
上一様に絶対収束するが, ![]() が十分に大きいならば,残差は任意の固定された
が十分に大きいならば,残差は任意の固定された ![]() に対して,オーダー
に対して,オーダー ![]() を持つことがある.なぜ近似が成功していないのか?
を持つことがある.なぜ近似が成功していないのか?
第十三節
![]() の指数級数展開を考えることで,
の指数級数展開を考えることで, ![]() との差が漸近的に縮まる,とは限らないことを十二節でみた.
との差が漸近的に縮まる,とは限らないことを十二節でみた.
この節では「漸近表現」の考え方を少し変えることでこれを解決する.次節ではこれをさらに精緻化しよう.
以降,添字が多くなることを回避するため ![]() は同分布としよう.このとき,次が成り立つ.
は同分布としよう.このとき,次が成り立つ.
任意の ![]() と
と ![]() とについて,
とについて, ![]() が成り立つならば,
が成り立つならば,
![Rendered by QuickLaTeX.com \[\int^\beta_{-\beta}\cdots\int^\beta_{-\beta}\left(W(z)-\Phi(z)-\sum_{\nu=3}^{3h}\frac{c_\nu}{\nu!}\Phi^{(\nu)}(z)\right)dt_1\cdots dt_h=O\left(\frac{\log^2n}{n^{\frac{h+1}{2}}}\right),\qquad z=x+t_1+\cdots+t_h.\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-23b539aab40645d7a15dcd09953061e2_l3.png)
が ![]() 上一様に成り立つ.
上一様に成り立つ.
この定理からまず, ![]() を1つ大きく取る毎に,指数級数展開の項を新たに
を1つ大きく取る毎に,指数級数展開の項を新たに ![]() つ考慮に入れる必要が生じることが判る.
つ考慮に入れる必要が生じることが判る.
次に,
![Rendered by QuickLaTeX.com \[\Phi(x)+\sum_{\nu=3}^{3h}\frac{c_\nu}{\nu!}\Phi^{(\nu)}(x).\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-d6611220453402854600b85c6809c342_l3.png)
を ![]() の代わりに使うことで,
の代わりに使うことで, ![]() に向けた平滑化に成功する,ということが保証されたことにもなる.
に向けた平滑化に成功する,ということが保証されたことにもなる.
このあと証明の概略が述べられるが,特性関数のことを adjunct of the probability function と表現していることが興味深く,式も
![]()
と表されている.
この定理は,所望のオーダーでの近似がほしいならば ![]() 重積分が必要である,という意味で本質的である.
重積分が必要である,という意味で本質的である.
第十四節
![]() が追加の条件を満たすならば,
が追加の条件を満たすならば, ![]() の通常の意味での「漸近展開」が得られる.
の通常の意味での「漸近展開」が得られる.
引き続き同分布の仮定の下で,典型的な根源誤差を ![]() とおく.これについて,次が成り立つ:
とおく.これについて,次が成り立つ:
![]() が存在し,
が存在し,
![]()
を満たすならば,任意の ![]() に対して,
に対して,
![Rendered by QuickLaTeX.com \[\left|W(x)-\Phi(x)-\sum_{\nu=3}^{3h}\frac{c_\nu}{\nu!}\Phi^{(\nu)}(x)\right|<Kn^{-\frac{h+1}{2}}e^{-\frac{x^2}{4}}.\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-3017d9a46c72445682661c0f50ff008f_l3.png)
が成り立ち, ![]() は
は ![]() と独立に取れる.
と独立に取れる.
第十五節
根源誤差の仮説に関連して,Charlierはまた別の種の級数を考案した.本人は B-級数と呼んでいる.一般的な枠組みでは,次のように述べられる.
対象はやはり
![]()
の形で表される変数である.この分布関数を ![]() で表す.しかし,
で表す.しかし, ![]() の分布関数については,同分布とはせず,次のような緩い依存関係を想定する.
の分布関数については,同分布とはせず,次のような緩い依存関係を想定する. ![]() を定数,
を定数, ![]() を別の分布関数として,
を別の分布関数として,
![]()
とする.すると,各分布関数 ![]() のFourier変換を
のFourier変換を ![]() で表すこととすると,
で表すこととすると,
![]()
![]()
を満たす.よってこの考察から,実部と虚部を ![]() と表すと,収束の問題がなければ,極限関数は
と表すと,収束の問題がなければ,極限関数は
![]()
と表せる.
例として, ![]() を取ると,これがCharlierが実際に考察した場合である.
を取ると,これがCharlierが実際に考察した場合である. ![]() となり,
となり,
![]()
と展開できる.この極限関数は, ![]() 上にジャンプを持つ階段関数で,
上にジャンプを持つ階段関数で, ![]() における跳躍は
における跳躍は
![]()
で表される. ![]() の
の ![]() におけるジャンプの大きさの漸近表現は
におけるジャンプの大きさの漸近表現は
![]()
となる.ここに ![]() の積分表示を代入したものが,CharlierがB-級数と呼ぶ所のものである.実際の応用上では極めて有用であることが判っている.しかしSteffensenが指摘しているように,
の積分表示を代入したものが,CharlierがB-級数と呼ぶ所のものである.実際の応用上では極めて有用であることが判っている.しかしSteffensenが指摘しているように, ![]() の積率は発散し得ることが理論的な障壁である.
の積率は発散し得ることが理論的な障壁である.
コメント