次の人類学の論文の内容を紹介します．
Kenji Itao, Kunihiko Kaneko. (2020) Evolution of kinship structures driven by marriage tie and competition. Proceedings of the National Academy of Sciences 117(5) 2378-2384
この論文などの成果により，著者の板尾健司さん（@k_itao_0906）は「多階層進化モデルによる社会構造の生成」の推薦題目で，東京大学総長賞を受賞しました．分類としては人類学の節に掲載された論文ですが，数理モデルを用いた理論面についての研究です．論文内のdiscussion sectionの締め括りでは，この種の研究が，社会人類学全体を理論的に基礎づける普遍的な役割を果たす可能性が示唆されています[1]．東京大学HPでも，「レヴィ=ストロース70年来の謎を進化シミュレーションによって解明」と紹介されています．
筆者には，この著者の方のツイートの通り，「フィールドワークなどの人文学的研究から提出された結果に対して，数理的に説明がつくところに対しては数理から部分的な理由づけを与え，その補助線に沿って内容を詰める」と言った数理と人文の協業に理想的なものを感じ，そして内容もまさに謎解きのような，非常に野心的な内容に思われましたので，以下に概説を試みます．
用語の解説
社会人類学における伝統的な用語を紹介してみます．が，むしろこれらの概念を数値シミュレーションの結果から捉え直すという内容の論文ですので，あまりピンと来ずとも，用語間の関係性だけ掴んで，論文の内容に入りましょう．
- リネージ(lineage)：先住民社会に存在する，祖先を共有する複数の家族から成る共同体のこと．
- クラン(clan)：複数のリネージが構成する文化的に均質な生活共同体のこと．
- クランではいくつかの道徳律が周知されており，例えば結婚相手の選好も，当人がどのクランに所属するかに大きく依存する．
- 例えば「どのクランの相手と結婚するか」や，「その子供はどちらのクランに所属することになるか」などの道徳律である．
- また，同じクラン内での結婚は（必ずしも親等が近いわけではない場合も）比喩的な意味での「近親相姦」としてタブーとされている．これをインセストタブーという．”siblings as a category”（「カテゴリーとしての兄弟姉妹」）と言えるこの拡張された捉え方は，遺伝的な問題というよりも文化的な役割を持つ可能性が考えられる．
- クランではいくつかの道徳律が周知されており，例えば結婚相手の選好も，当人がどのクランに所属するかに大きく依存する．
- 親族構造(kinship structure)：社会の中での婚姻・親族関係の総体のこと．基本的には，クラン同士の相互作用によって構成されると考えられる．先住民の社会の多くでは社会構造の基礎を作る．
- 競争(conflict)：協力(cooperation)の対義語．殺人が代表的な競争である．
- 配偶競争と言った場合は，配偶者の競争に起因した紛争のことなどを含めて表す．
Lévi-Straussの分類に基づき，親族構造の例は，次の４つに分類できる．
「レヴィ=ストロース70年来の謎を進化シミュレーションによって解明」する前に，謎の内容を確認します．レヴィ=ストロースは，博士論文でもある著書『親族の基本構造』の中で，インセストタブーの発見を報告し，親族構造を大きく４つに分類し，「なぜ（遺伝的な危険性がなくとも）インセストタブーが存在するのか？」「なぜ特定のクランとのみ結婚するような親族構造となっているのか？」という謎を提起しました．当論文では，図式を用いて，４つの親族構造の分類が整理されていました．また，数学的に整理された定義も紹介されました．この２つを紹介します．
をクランとして，
記号
は，クランX出身の女性はクランYの男性と結婚することを表し，
記号
は，クランX出身の男性の子供はクランYに帰属される社会規範が存在することを表す
とする．また，クランの名前で
とは，ローマ字
は父の出身クランを，右下添字
は母の出身クランを表し，それらの子供のなすクランとした．
１．インセスト構造(incest structure)：ただ一つのクランをもち，その中で結婚と出産と子育てがなされる共同体．従ってincest tabooを持たない．
![\[\xymatrix{ A\ar@(ul,dl)[]\ar@(ur,dr)@{=>}[]}\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-a95e57a88f9af50dd3239c17fd012657_l3.png "Rendered by QuickLaTeX.com")
２．双分組織(dual organization)：２つのクランをもち，互いにもう片方のクランの相手と結婚し，子供は母の出身であるクランに所属するとみなされる共同体．
![\[ \xymatrix{ A\ar@(ul,dl)[]\ar@{<=>}[r]&B\ar@(ur,dr)[]} \]](https://anomath.com/wp-content/ql-cache/quicklatex.com-8a9c494fe19774877d857790b499992e_l3.png "Rendered by QuickLaTeX.com")
３．限定交換(restricted exchange)：２つのクランの間のみで閉じた直接的な新婦の交換(direct exchange)が行われ，また子供の帰属もクランを行き来するような親族構造のこと[5]．
一般に権力差の少ない平等な社会となる．オーストラリアのAboriginalやアマゾンのYanomamoなどの狩猟採集社会で見られる．
![\[\xymatrix{ &&A_1\ar@{<=>}[rrr]\ar@{<->}@/_1pc/[dr]&&&B_2\ar@{<->}@/^1pc/[dl]\\ A_1\ar@{<=>}[r]\ar@{<->}@/_1pc/[d]&B_2\ar@{<->}@/^1pc/[d]&&A_2\ar@{<=>}[d]&B_1\ar@{<=>}[d]\\ A_2\ar@{<=>}[r]&B_2&&D_1\ar@{<->}@/_1pc/[dl]&C_2\ar@{<->}@/^1pc/[dr]\\ &&D_2\ar@{<=>}[rrr]&&&C_1}\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-5e96084508ed7dc2f2f96eeaabf37da0_l3.png "Rendered by QuickLaTeX.com")
４．一般交換／全面交換(generalized exchange)：複数のクランの間で新婦を間接的に交換する(indirect exchange)親族構造のこと．従って，
という形の矢印を持たず，新婦の流れは循環する．
一般に社会的地位の格差が見られる，比較的平等主義的でない社会(non-egalitarian society)となる．インドや中国，ミャンマーのKachinなどの農耕社会や，ロシアのNivkhなどの漁労社会で見られる．
![\[\xymatrix{ A\ar@{=>}[rr]\ar@(ul,dl)[]&&B\ar@{=>}[dl]\ar@(ur,dr)[]&&A\ar@{=>}[r]\ar@(u,l)[]&B\ar@{=>}[d]\ar@(u,r)[]\\ &C\ar@{=>}[ul]\ar@(dr,dl)[]&&&D\ar@{=>}[u]\ar@(d,l)[]&C\ar@{=>}[l]\ar@(d,r)[]}\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-514bb795379121996c1e8d96af465a7a_l3.png "Rendered by QuickLaTeX.com")
これらの４分類は，「道の長さ」に注目すると，数学的に明確に特徴付けることができる．
矢印
を繋いで得られる巡回道(marriage cycle)の最大の長さを
，矢印
を繋いで得られる巡回道(descent cycle)の最大の長さを
とすると，これらを用いて次のように定義できる．
の場合をインセスト構造と呼ぶ．
の場合を双分組織と呼ぶ．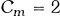
かつ
の場合を限定交換と呼ぶ．
かつ
の場合を一般交換と呼ぶ．
なお，人類学用語では，であることを，unilineal decent（単系制）といい，であることを，bilateral descent（双系制）という．
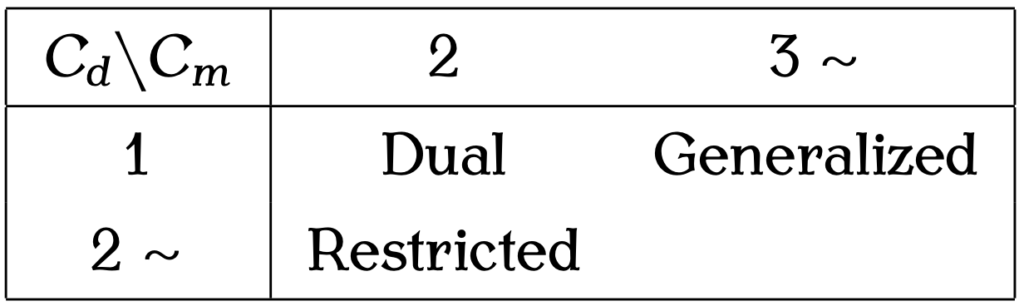
このように整理されると，
に当たるものはなんと呼べばいいのか，と欠けた部分が発見しやすくなるだろう．実際，このような構造は自然界でほとんど見られないので定まった名前はついていない．[4]
結果
さて，レヴィ=ストロースが報告した観察結果に対し，「どうして親族構造には種々のバリエーションがあるのか？」「なぜ一見不合理なインセストタブーが存在するのか」の謎に迫る段階が来ました．この論文の肝である進化シミュレーションにより，どのような結果が得られたか昇華します．レヴィ=ストロースが定義した親族構造を，シミュレーションにより再現できれば，理解が進むかも知れない，という算段です．
これらの親族構造がどのような条件で創発されるかを調べるために，共同体レベルでの多階層進化を採用した，先住民社会の２つのモデル（エージェント・ベースド・モデル）を用意する．
各リネージは形質
と配偶者選好
との２つの変数を持ち，次の条件を満たして振舞う．
- 形質は，似たような形質を持ったリネージの間に協力を誘発する．
- 配偶者選好は，似たような選好を持つリネージの間に競争を誘発する．
- リネージ間に結婚が起こると，協力が誘発される．
- 続いて，多階層Moran過程(hierarchical Moran process)と呼ばれる確率過程を用いて，適応度の低いリネージ（あまり人口の増えないリネージ）は，共同体のレベルで淘汰されるようになっている．
- インセストタブーを持ったクランの創発が確認された．具体的には，リネージは
-空間上で複数のクラスターを形成して集合するのが確認され，それぞれのクラスターは内部では結婚が起こらず（インセストタブー），特定の他のクラスターの人間と結婚するようになることが観察された．従って，このクラスターが「インセストタブーを持つクラン」と呼ぶべきものに当たることが分かる． - 同じクラスター内のリネージは協力し合うようになり，結婚相手のクラスターに所属するリネージとも協力するようになるが，同じクラスター内には配偶競争が起こる．
しかし，このモデルでは，限定交換や一般交換などのより洗練された親族構造の創発は確認されなかったので，一つ変数を増やし，「父親からの継承」と「母親からの継承」とに対応した２つの変数を備えたモデルで検討する．
各リネージは２つの形質
と２つの配偶者選好
の変数を持ち，次の条件を満たして振舞う．
- 形質は，似たような形質を持ったリネージの間に協力を誘発する．
- 配偶者選好は，似たような選好を持つリネージの間に競争を誘発する．
- リネージ間に結婚が起こると，協力が誘発される．
- 続いて，多階層Moran過程と呼ばれる確率過程を用いて，適応度の低いリネージ（あまり人口の増えないリネージ）は，共同体のレベルで淘汰されるようになっている．
- 「協力が強く要請される」環境においては，双分組織が生起しやすい．
- その中でも，配偶競争が厳しくなるにつれて，順に，全面交換，限定交換が双分組織に取って代わるようになる．
この結果は，限定交換や一般交換の親族構造の地理的分布について，部分的な根拠になっていると言えるだろう．実際，アボリジニやヤノマミ族についての研究では，配偶競争がリネージ間の紛争を引き起こすことが報告されているが，農耕社会では，土地や食糧のための戦争を起こすためにも，大規模な協力を必要とする．漁労社会でも，漁をする縄張りの確保や漁業のためには協力を必要とする．
詳細な結果は[2]参照．
評
「どうしてそうなっているのか？」という根源的な謎が，数理的には「自然」だと理解できて，部分的に解決されたわけです．当論文内でも，「このような生成モデルによる理論的研究は，人類学の分野に普遍理論を敷くポテンシャルがある」，と議論されています．
- Discussion sectionの締め括りでは，この種の生成モデルによる理論的研究が，社会人類学に普遍理論を提供する足掛かりになるかもしれないことが示唆されている．実際，各地域での比較の研究はなされてきたが，その生成元理についての研究は，このような数理を用いない限り達成され得ないだろう．これは親族構造についての普遍的な原理を暴き出すから，著者らが「普遍人類学」と呼ぶべき研究分野が創立されてもおかしくないかもしれない[1]．
- Lévi-Straussは参与研究により，複雑な総体としての文化に向き合って，フィールドワークから人類学的研究を遺した，構造主義の創始者の一人である．その際に，「親族は新婦を交換するために構造化する」ということを，同時代の数学者であるAndré Weilに協力を仰いで，新婦の交換を置換群に見立てて解析している（『親族の基本構造』第14章）．従って，今回の研究は筆者には，本質的に数理的な行為を，70年越しに数理が回収したようにも思える[3]．
- しかし，回収しただけでなくこの研究は，構造を静的に解析したWeilの見方に加え，「いかにしてそのような構造が生起するか」という新たな問題に向き合っており，環境に依存して「立ち現れては消えていくもの」としての構造の動的な見方とそのための道具を提供している．これにより，構造主義の文脈でも，新たな議論の可能性を拓く強固な基点となり得る．
- その結果この研究は，「どうしてこのような構造が生まれるのか」という”Why?”の問題に対してさえも，必要な環境要因を探すという形で部分的な理由づけを与える構造になっている．このような訴求力を持つ「理由づけ」を鮮やかに繰り出せることは数理の特徴だろう．この場合もまた，この結果の上には新たな言論空間が広がり，従来の知的文脈にもこの結果が反射することとなる．特に地理的分布を今回の結果から説明できないか，など，新たな研究の余地が広がる．このように，筆者は「数理で語るべきところは数理で語り，日本語で語るべきところは日本語で議論する」というような，新たな形の学問を夢想するのである．
注
In addition to field studies, theoretical studies by simple constitutive models, as we present here, will open a door for social anthropology to construct a general theory therein.
Evolution of kinship structures driven by marriage tie and competition Kenji Itao, Kunihiko Kaneko.
この新たな学問分野として想定できる展望を，普遍人類学と呼んでいるようです．
本研究成果は計算機を用いて人間社会の普遍的な構造を論じ、人類学の理論研究の新たな方法として普遍人類学の展望を示すものである。
レヴィ＝ストロースの70年来の謎を進化シミュレーションで解明（研究成果）
これについて筆者は，近年の進化心理学の状況と似た状況を見出します．日常で使うことばが持つ訴求力に頼り切るのではなく，論理の構築には数理のことばを用いる．我々筆者はこの「日本語」と「数学語」の素敵な協業に，将来性を見出さずにはいられないのです．戻る．
２．以下に，より詳しく，当該論文の内容をかいつまんで記述します．さらに詳しくは当該論文を是非．コードもGitHub上で公開されています．
モデルの設定
- パラメータの空間
![[0,1]^2](https://anomath.com/wp-content/ql-cache/quicklatex.com-7cf365645be1696ea719ac40c2f7490b_l3.png "Rendered by QuickLaTeX.com")
内の50個の点からなるリネージの集合![I\subset [0,1]^2](https://anomath.com/wp-content/ql-cache/quicklatex.com-f3c68003c465678948dbf369de56ced3_l3.png "Rendered by QuickLaTeX.com")
を定め，このようなリネージの集合を100用意する． - 各リネージ
![i=(t_i,p_i)\in [0,1]^2](https://anomath.com/wp-content/ql-cache/quicklatex.com-5340b5a2bd84a419d633d3672901d574_l3.png "Rendered by QuickLaTeX.com")
は初期人口から２倍の人口になると，２つのリネージに分裂し，それぞれのパラメータは![\eta\in[-\mu,\mu]\;(\mu>0)](https://anomath.com/wp-content/ql-cache/quicklatex.com-764fb46fc792e8dd3b354120c269bcda_l3.png "Rendered by QuickLaTeX.com")
だけ変化する．また，人口が0となったリネージは消滅する． - コミュニティも同じ変化をするが，２つに分裂した瞬間，より適応度の低い方がhierarchical Moran過程で選出され，そちらがシステムに消去される（マルチレベル選択）．
- リネージ
間は，
が十分小さい場合に協力する．第一項が小さいための協力は近親性により起こり，後二項が小さいための協力は結婚成立のために起こる．また，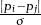
が十分小さい場合は，配偶競争が起こる． 
を協力が引き起こす人口増加率の因子，
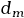を競争が引き起こす人口減少率の因子とする．
結果と議論
- one-trait modelでは，
が十分大きい時，配偶交換を行うクラスター群の出現が観測された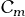．は様々であったが，であった． - two-trait modelでは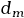，が十分大きい時に双分組織の構造が観察され，引き続いて一般交換と限定交換が観察されたが，も大きいとそのクラスター群は絶滅した．比
が十分大きい時には双分組織から一般交換を経て限定交換に至る構造変化が見られたが，比がそれほど大きくない場合は一般交換が観察されるのみで止まった．が大きい場合は，配偶競争を避けるためにライバルとなるクラスターが少ない状態で安定となるためである．また，
が大きい場合は，リネージ間の関係性の変化も激しいためクランの間の関係性も脆弱で，限定交換の関係性は一般交換の構造に取って代わられる． - パラメータの変異因子は，学校教育の制度があるなど，中央集権的で，両親からの文化的影響が比較的小さい社会では大きくなる．この場合，安定した親族構造は見られなかった．一方，が小さい場合は，インセストタブーと，より洗練された親族構造の出現が観察された．
同時代を生きた数学者であるAndré Weilは，Nicolas Bourbakiと呼ばれる数学者集団を（Henri Cartanと）作り，数学原論と呼ばれる，今まで誰も見たことのなかったスタイルでの数学の教科書を執筆する野心的なプロジェクトを進め，これは現在まで続いている．この数学原論は現在計11部門に分かれており，数学の多くの分野に渡る大著であるが，その核としては，３つの「構造」を中心として公理論を据え，数学全体をいくつかの公理から展開する形で執筆された．この書籍群の現代数学への影響は計り知れず，現代の数学の基調をなして全世界の数学事情に溶け込んでいると言える．
構造主義という用語が広く知られるようになったのは、クロード・レヴィ＝ストロースが、このような方法論を人類学に応用し、文化人類学において婚姻体系の「構造」を数学の群論 (group theory) で説明したのが嚆矢である。群論は代数学（抽象代数学）の一分野で、クロード・レヴィ＝ストロースによるムルンギン族の婚姻体系の研究を聞いたアンドレ・ヴェイユが群論を活用して体系を解明した。
https://ja.wikipedia.org/wiki/構造主義
構造主義は発生当初において群論との関係が深いことは前述した．ここで，当該論文の挿入図が，圏論の図式のように見えることは，注目に値する可能性がある．なぜならば，圏論も発生当初において，群論との関係が深いからである．さらに，
原則として要素還元主義を批判し、関係論的構造理解がなされる。ソシュールが言語には差異しかないと述べたと伝えられているように、まず構造は一挙に、一つの要素が他のすべての要素との関係において初めて相互依存的に決定されるものとして与えられる。このような構造の理解においては、構造を構成する要素は、原則として構造を離れた独立性を持たない。
https://ja.wikipedia.org/wiki/構造主義
という構造主義に対する説明は，群論というより，圏論において最も理想的な形で実現されているように思える．実際，圏論を基調としたブルバキの『数学原論』あとの数学は，次のように説明されることもある：
現代の数学では，数学の対象を単独に扱うのではなく，それと似た対象全体のなす圏の一員として捉えることが多 い.こうすることで，対象自体の構成よりも，圏の中の他の対象との関わりに焦点が当たる．圏の個々の対象ではな く，圏自体が興味の主な対象となることもある．圏の中の役割によってその対象が特定されることを示すのが，米田 の補題と呼ばれている命題である．
斎藤毅『数学原論』(2020)
＊ここにおいて，Bourbakiの数学原論と，日本の数学者・斎藤毅先生の『数学原論』が，群論と圏論との対比の裏に交錯していることも，注目に値するかもしれない．戻る．
４．レヴィ=ストロースはムルンギン族の婚姻体系がこれに当たるとしたが，後に一般交換の一種であることが判明した．戻る．
５．「２つのクランの間のみで閉じた直接的な新婦の交換が行われること」即ちを明確に定義とし，双分組織まで含めて「限定交換」に含める立場もあるが，ここでは当論文で採用されていた定義に従った．戻る．
コメント