経済学研究科で開講された測度論的確率論の授業で次のような問題が宿題として出題された．
- Define
.- (a) Show that
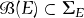. - (b) Show that
. (Hint: use the inclusion 
)
- (a) Show that
- Assume
. Show that 
is represented as![\[\mathcal{B}(E)=\{A\mid A\in\mathcal{B}_d,A\subset E\}.\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-80c587cb0f09aea2265e9b8963579dd6_l3.png "Rendered by QuickLaTeX.com")
僕が用意した答案は次の通りである（読み飛ばしてOK）．
- (a) First we show (1)
, and then (2) 
is a 
-algebra. From these two facts, we can conclude from the minimality of ,![\[\mathcal{B}(E)=\sigma(\mathcal{O}(E))\subset\Sigma_E.\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-7d80ace25fce3f5789dfe2232650ed72_l3.png "Rendered by QuickLaTeX.com")
- (1) Let
be fixed．By the definition of relative topology, there exists an open set 
such that 
. Therefore, 
． - (2) The inclusion map
is clearly measurable, which allows us to safely apply the result in Homework No.1. As a result, we can conclude that
is a![\[\{f^{-1}(A)\mid A\in\mathcal{B}_d\}=\{A\cap E\mid A\in\mathcal{B}_d\}=\Sigma_E\]](https://anomath.com/wp-content/ql-cache/quicklatex.com-50cef37f05d12fc986a0ee573b6a898c_l3.png "Rendered by QuickLaTeX.com")
-algebra. We will call this a 
-induced -algebra and denote it by 
.
- (1) Let
- (b) Since we have shown that is the -induced -algebra, and since is
-measurable, it follows that 
.
- (a) First we show (1)
- We will prove
and 
.- (a) We have
because 
(combined with the minimality of ). To show the latter fact, we first fix (clearly 
). Then, using Part (i)(a)(1), 
and the right hand side is the intersection of two elements of 
. Therefore, 
. - (b) We have
because every 
satisfies 
and , which are precisely the conditions for being a member of .
- (a) We have
これは問題文の誘導に乗って答えたために，非常に変な議論になっている．本質的な所をごまかして，非本質的な所に語数を費やすことで，「宿題」として点が来そうにまとまったが，とても数学的に良いとは言いたくない．実際頭を捻って読んでみた読者も，何を示したのかよくわからないだろう．第１問の本質は，相対位相がそもそも包含写像 
による始位相として定義されている（例えば斎藤毅『集合と位相』p.94）から， 
による 
の引き戻しと 
の相対位相が生成するBorel -代数とが一致することは当然のことである（と言ってしまうと問題の意義を問うているように聞こえるかもしれないが，当然の数学的事実はその当然さが誰の目にも判るような証明を与えるのが理想と言えるだろう．実際この問題は定義の理解を確認するに素晴らしい問題だと思われる）．だから，そもそも と とに議論を分解している時点で筋が悪いと言えるかもしれない．
この授業では位相の議論を一切しておらず，相対位相の定義も明示的に議論することが躊躇われたため， 「は明らかに可測」という表現で済ましていた．本当はこの点を深掘りすることで，より簡潔な証明（２行くらいの）になるのであるが．
そこで，僕は身の処し方がわからなくなる．自分は「問題に不備があれば，それを指摘し，適切に修正して，その自分で修正した問題を解くことまで含めて解答である」と教わってきたから，必要に応じて相対位相の定義を確認し，「両方とも を可測にする最小の -代数である」として特徴付けられることから 
を得てから，小問の(a), (b)は誘導に乗らずに結論を得た，という答案を作りたかった．だが，今回は自分で履修しているわけではなく，友人にアドバイスをしているだけの立場なので，実際にそうはせず，ただこのブログに書いている．
本当は書きたかった解答（日本語で行きます）
- とは包含写像 による の引き戻しである：
．よって， を可測にする最小の -代数として特徴付けられるが，これは相対位相 
は が定める始位相として定義されることを思い出せば， を特徴付ける性質でもある．よって ．
第２問は気が向いたらコメントします．
みんなならどうする？数学を貫く？最初に思いついた解答を書いて提出してしまう？
コメント